Real Gases

Most of the discussions of gases assume that the gases exhibit ideal behavior. Ideal behavior involves two things: the first is that the gas can be infinitely compressed or infinitely cooled and the gas will not liquefy. The second is that the gas molecules have no volume. With these assumptions, the ideal gas law, PV=nRT, can be used.

In reality, however, if a gas is compressed enough the particles will attract and will liquefy. Similarly if the gas is cooled to its boiling point, it will liquefy. Therefore at low temperatures or high pressures, the effect of the attractive forces becomes larger. However, if the gas is moving fast enough, attractive forces between the molecules that cause liquefaction are not a factor.

Gas molecules also definitely have a volume, small though it may be, and the volume of the molecules play a factor under conditions of large gas molecules and small container volumes.

Joseph van der Waals studied the behavior of real gases and made comparisons to the ideal gas law. He derived an equation to account for the differences. The equation adds in two constants, a and b, to the ideal gas law. These constants are derived to give the best agreement between the observed behavior and the equation. Therefore each gas has its own values for the constants. The van der Waals equation is stated as:

P + n²a/V² deals with attractive forces between molecules and how they reduce the ideal pressure. V - nb accounts for volume of the particles, where the constant b is related to the size of the molecule and since the molecules take up space, the effective size of the container is decreased. Van der Waals received a Nobel Prize in physics in 1910 for his work in gases and liquids. Below is a table giving the a and b constants for various gases. The a values are small for those gases with small intermolecular attractions, such as He. In general the larger molecules have a larger b constant, as can be seen for octane, though this is not the only factor for determining b.

Gas	Formula	a [(L² · atm)/mole²]	b [L/mole]
Helium	He	0.03412	0.02370
Hydrogen	H₂	0.2444	0.02661
Nitrogen	N₂	1.390	0.03913
Oxygen	O₂	1.360	0.03183
Carbon dioxide	CO₂	3.592	0.04267
Acetylene	C₂H₂	4.390	0.05136
Chlorine	Cl₂	6.493	0.05622
n - Butane	C₄H₁₀	14.47	0.1226
n - Octane	C₈H₁₈	37.32	0.2368

To illustrate the differences between the two equations, an example using acetylene and helium gas will be shown.
Example: One mole of acetylene gas is placed in a 20.0 L container at 25 °C.

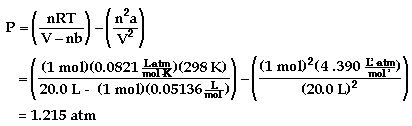
There is approximately a 0.66% difference between the two values. If the same calculation was done with helium gas, the difference would only be about 0.13%.

Return to Unit 1: Basic Principles

The Behavior of Gases

Real Gases vs. Ideal Gases