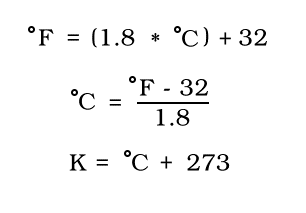
The Metric System is the most commonly used mesurement system in the world and in the scientific community. The metric system uses the units in the chart for measurement.
| Unit | What it Measures |
|---|---|
| Meters | Distance |
| Liters | Volume |
| Grams | Mass |
| Second | Time |
| Kelvin | Temperature |
Kelvin? What's that you say? Kelvin is the unit that is used in most calculations in Chemistry. Celcius is also often used because of its easy conversion to and from Kelvin. Fahrenheit is the most common scale in the U.S., so converting among all three is necesssary.
The generic equations are as follows: 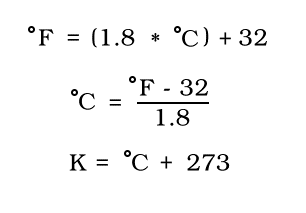
Example:
Note: Kelvin does not have a degree mark nor is it said with a degree.
One of the many reasons the metric system is used is for its easy ability to add prefixes that change the value of the unit. For example: the prefix kilo- on grams means that 1000 grams equals 1 kilogram. In the example the prefix mulitiplied the original unit's value by 1000 because that is what kilo- stands for. The chart shows the most used prefixes in italics and the least used in regular print. This chart can be used to find the prefix of whatever unit you are working with.
| Prefix | Mulitplied By | Symbol |
|---|---|---|
| exa | 1018 | E |
| peta | 1015 | P |
| tera | 1012 | T |
| giga | 109 | G |
| mega | 1000000 | M |
| kilo | 1000 | k |
| hecto | 100 | h |
| deka | 10 | dk |
| deci | .1 | d |
| centi | .01 | c |
| milli | .001 | m |
| micro | 10-6 | µ |
| nano | 10-9 | n |
| pico | 10-12 | p |
| femto | 10-15 | f |
| atto | 10-18 | a |
* If you are not using Netscape, the numbers that are after the 10 in the chart are superscripts
If you wanted to know how many meters are in 4 megameters the conversion chart could be consulted. You would discover that 1 megameter = 1000000 meters. So 4 * 1000000 = 4000000. Therefore 4 megameters = 4000000 meters. (This can also be accomplished by moving the decimal six places)
Other Examples:
Scientific Notation is a way to abbreviate very large or very
small numbers. The format of Scientific Notation is this: a
number that has a decimal after the first digit, mulitiplied by
ten with an exponent. An example is: 1.23 X 104. The
exponent can be positive or negative. If the exponent is positive
then you move the decimal to the right by the number of the
exponent. If the exponent is negative then you move the decimal
to the left by the number of the exponent. This form of numbers
can express very large and small numbers depending on the
exponent. More examples are as follows.
| Scientific Notation | Regular Form |
|---|---|
| 1.23 X 104 | 12300 |
| 4.91 X 103 | 4910 |
| 2.1 X 10-3 | .0021 |
* If you are not using Netscape, the numbers that are after the 10 in the chart are superscripts
Significant Figures or Digits are the amount of digits that
are accurate in a calculation. This is determined by how many
digits there are in the numbers of the calculation. The rules for
determing how many significant digits are as follows:
* If you are not using Netscape, the numbers that are after the 10 in scientific notation are superscripts
The rules for determining the number of significant digits after a calculation are grouped by Addition and Subtaction, and Multipication and Division.
When two or more numbers are added or subtracted the final answer is rounded off to the same decimal place as the number having its last significant digit the furthest to the left.
Example:
If you have the numbers 4.501 and 90.2 added together you will get 94.7 because the last column that both numbers use is the tenths place.
Significant digits in Multipication and Division are determined by the number of significant digits in each of the numbers in the calculation. The answer must have the same amount of significant digits as the number in the calculation with the least amount of significant digits.
Example:
If you multiply the numbers 500 and 256 together the answer would be 100000 because 500 only has one significant digit so the answer can have only one significant digit.
If you divide 1575 (four significant figures) by 17.6 (three significant figures), you round your answer to 89.5 (from 89.48863) so that it will have 3 significant digits.
Dimensional analysis is a process that allows
changing of units. If you were going to change from centimeters
to meters Dimensional analysis allows an easy way to change. To
start you must decide what the conversion factor is, so we know
that 100 centimeters = 1 meter.
In Dimensional analysis you can setup the equation like this.
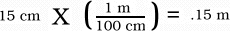
The centimeters are in the denominator of the conversion factor because the measurement is already in centimeters. The answer comes out in meters because the centimeters cancel in the division.
Other Examples:
13.1 g (1000mg / 1g) = 13,100 mg
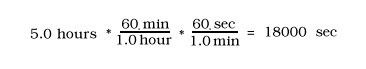
Metric System | Scientific Notation | Significant Figures | Dimensional Analysis | Top of Page | Science 10 | Donkistry